Число

Матеріал з Вікіпедії — вільної енциклопедії.

Число́ — одне з найголовніших понять математики, яке в багатьох випадках може виступати як міра кількості чогось.

У давнину у слов'янських мовах, слово "число" означало "знак", "символ", "поняття", "ідея"^{[Джерело?]}. Під словом "числити" розуміли в ті часи "значити", "думати", а також "записувати щось за допомогою знаків", "робити певні дії зі знаками". Пізніше, зокрема з поширенням арифметики і точних наук на Русі Петром I у XVIII ст. під числами стали розуміти в першу чергу ті знаки, які використовуються для позначення певних кількостей. У XIX та XX ст., з розвитком і поширенням вищої, теоретичної математики, слово "число" знову починає вживатися ширше - для назви знаків, позначень і понять, які позначають не лише кількості - комплексні числа. Те саме ми спостерігаємо з поняттями "числити", "числення" - матричне числення, варіаційне числення і т. д.

Типи чисел

Математики поступово розширювали набір усіх відомих чисел. Поява нових видів чисел і числення тісно пов'язана з розвитком людського суспільства. Разом з тим, на кожне розширення числової системи можна дивитися з математичної точки зору, обґрунтовуючи таке розширення, як правило, розширенням можливостей виконувати деяку математичну операцію.

Натура́льні чи́сла — числа, що виникають природним чином при лічбі. Це числа: 1, 2, 3, 4, … Множину натуральних чисел прийнято позначати знаком $\N.$

Існують два основних підходи до означення натуральних чисел:

числа, що використовуються при лічбі предметів (перший, другий, третій…) — підхід, загальноприйнятий у більшості країн світу; формалізованим різновидом цього підходу є аксіоматичне описання системи натуральних чисел за допомогоюаксіом Пеано.
числа для позначення кількості предметів (відсутність предметів, один предмет, два предмети…) — підхід, прийнятий у роботах Ніколя Бурбакі, де натуральне число означається як потужність скінченних множин; при такому підході, як правило, 0 відносять до натуральних чисел.

Від'ємні та дробові числа не є натуральними числами.

Множина натуральних чисел є нескінченною: для будь-якого натурального числа знайдеться інше натуральне число, більше за нього.

Натуральні числа можуть використовуватись для лічби (одне яблуко, два яблука, три яблука, …).

Історія натуральних чисел

Поняття натурального числа, викликане потребою лічби предметів, виникло ще в доісторичні часи. Процес формування поняття натурального числа тривав протягом усієї історії людства. На найнижчому етапі первісного суспільства поняття абстрактного числа не існувало. У свідомості первісної людини ще не сформувалося те спільне, що об'єднує наприклад, «три людини» та «три озера». Аналіз мов первісних народностей показує, що для лічби предметів різного типу використовувалися різні словесні обороти. Слово «три» в контекстах «три людини», «три човни» передавалося по-різному. Такі іменовані числові ряди були дуже короткими і завершувалися неіндивідуалізованим поняттями «багато», які також були іменованими, тобто висловлювалися різними словами для різних типів об'єктів, такими, як «натовп», «стадо», «купа» тощо.

Спочатку числові терміни мали якісніший характер — відрізняли один, два та більшу кількість. Більші числа одержувалидодаванням. Наприклад, в австралійського племені ріки Муррей, 1 — енза, 2 — петчевал, 3 — петчевал-енза, 4 — петчевал-петчевал. Але навіть такі здібності людство здобуло після великого проміжку часу, в який користувалися лише з понять «один», «два» та «багато» (ще й досі збереглося плем'я, яке зупинилося на цьому етапові розвитку вмінь числового абстрагування).

Джерелом виникнення поняття абстрактного числа була лічба предметів, що базувалася на зіставленні предметам даної сукупності предметів певної сукупності, що мала роль еталону. У більшості народів першим таким еталоном були пальці («лічба на пальцях»), що безпосередньо підтверджується мовознавчим аналізом назв перших чисел. На цьому етапі число стає абстрактним, незалежним від якості об'єктів лічби, але разом з тим пов'язаним з природою сукупності-еталону. Розширення потреб лічби спонукало людей користуватися з інших еталонів лічби, наприклад, зарубок на паличці. Для фіксації порівняно великих чисел стала використовуватися нова ідея: позначення деякого певного числа (у більшості народів — десяти) новим знаком, наприклад, зарубкою на іншій паличці.

З розвитком писемності можливості відтворення чисел значно розширились. Спочатку числа стали позначати рисками на матеріалі, що слугував для запису (папірус, глиняні таблички тощо). Потім були введені інші знаки для великих чисел.Вавилонські клинописні позначення чисел, а також «римські цифри», що збереглися до наших днів, ясно свідчать саме про цей шлях формування позначень для чисел.

Великим прогресом було винайдення «цифр». Тепер стало можливим записати будь-яке число обмеженим набором символів. Наприклад, вавилоняни розвинули потужну позиційну систему, що базувалася на цифрах 1 та 10, але фактично її основою було число 60. Зручнішою була індійська позиційна система числення, що дозволяла записати будь-яке натуральне число за допомогою десяти знаків — цифр; вона згодом стала всесвітньо визнаною і досі залишається такою (хоча форма цифр дещо змінювалася; цифри цієї системи ми називаємо арабськими, оскільки система прийшла в Європу через арабів). Таким чином, паралельно з розвитком писемності, поняття натурального числа приймає все більш абстрактну форму, відокремлену від будь-якої конкретності поняття числа, відтворюваного як у формі слів в усній мові, так і в формі позначення спеціальними знаками в письмовій.

Важливим кроком у розвитку поняття натурального числа є усвідомлення нескінченності натурального ряду чисел — потенційної можливості його безмежного продовження. Чітке уявлення про нескінченність натурального ряду відображене в пам'ятниках античної математики (III століття до н.е.), у працях Евкліда й Архімеда. У «Началах» Евкліда встановлюється навіть нескінченність кількості простих чисел, а у книзі Архімеда «Псаміт» — принципи для побудови назв та позначень як завгодно великих чисел, зокрема більших за «число піщинок у світі».

Нуль, спочатку означав відсутність числа; він став розглядатися як число лише після введення від'ємних чисел нуль іноді включають до натуральних чисел).

Питання про обґрунтованість поняття натурального числа довгий час у науці не ставилося. Поняття натурального числа настільки звичне і просте, що не виникало потреби в його означенні в термінах будь-яких простіших понять. Лише в серединіXIX століття, під впливом розвитку аксіоматичного методу в математиці з одного боку, і критичного перегляду основматематичного аналізу — з іншого, назріла необхідність обґрунтування поняття кількісного натурального числа.

Чітке означення поняття натурального числа на основі поняття множини було дано в 70-х роках XIX століття в роботах Георга Кантора. Спочатку він означує рівнопотужність множин. Потім число елементів однієї множини означається як те спільне, що має дана множина і будь-яка інша, рівнопотужна їй, незалежно від якісних особливостей елементів цих множин. Таке означення відображає суть натурального числа як результату лічби предметів.

Інше обґрунтування поняття натурального числа базується на аналізі відношення порядку слідування, яке може бути задано за допомогою аксіом. Побудована на цьому принципі система аксіом була сформульована Джузеппе Пеано.

Ці́лі чи́сла — в математиці елементи множини $\Z = \lbrace \ldots -3, \, -2, \, -1, \, 0, \, 1, \, 2, \, 3 \, \ldots \rbrace$ яка утворюється замиканням натуральних чисел відносновіднімання. Таким чином, цілі числа замкнуті відноснододавання, віднімання та множення.

Множина цілих чисел складається з

множини натуральних чисел $\N$ ,
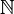нуля — розв'язку 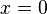$x=0\,$ рівняння $a+x=a,\ a\in \N$ ,
множини від'ємних чисел - множини розвязків $x=-a\,$ усіх рівнянь виду $a+x=0,\ a\in \N$ .

Цілі числа на числовій прямій.

Алгебраїчні властивості

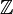$\Z$ не є замкнута відносно ділення двох цілих чисел (наприклад, 1/2).
$(\Z,+)$ є абелевою групою.
$(\Z, *)$ є комутативним моноїдом.
$(\Z,+)$ — єдина нескінченна циклічна група.
$(\Z,+,*)$ є комутативним кільцем (це слідує з двох вищеперечислених властивостей).
$(\Z,+,*)$ не є полем. Найменше поле, що включає цілі числа є множина раціональних чисел $\Q.$

Теоретико-множинні властивості

$\Z$ — зліченна множина.
$\Z$ — лінійно впорядкована множина без верхньої та нижньої межі.

Ознаки подільності чисел в десятковій системі

Ціле число ділиться націло на:

2, якщо остання цифра парна;
3, якщо сума цифр ділиться на 3;
4, якщо число з останніх двох цифр діляться на 4;
5, якщо остання цифра — 0 або 5;
6, якщо число ділиться на 3 і на 2;
8, якщо число з останніх трьох цифр діляться на 8;
9, якщо сума цифр ділиться на 9;
10, якщо остання цифра — 0.

Раціональні числа — в математиці множина раціональних чисел ℚ визначається як множина нескоротних дробів із цілим чисельником і натуральним знаменником:

$\Q = \left\{ \frac{m}{n}, m \in \Z, n \in \N \right\}$

або як множина розв'язків рівняння

$nx=m, \quad n \in \N,\quad m \in \Z$ ,

тобто n — натуральне число, m — ціле число.

Множина раціональних чисел є підмножиною алгебраїчних та дійсних чисел.

Назва цих чисел походить від латинського "ratio" - "відношення", у зв'язку з тим, що ці числа з часу своєї появи позначаються за допомогою відношення двох цілих чисел наприклад, 2:5 або 2/5. Інша назва - "дроби", тобто числа, якими можна позначити нецілу кількість предметів - півтора, третину стакана, чверть години і тощо. Під дробовими числами, як правило, розуміють ті раціональні числа, які не відносяться до цілих.

Поява раціональних чисел також дала змогу вирішити велику кількість прикладних задач із різних галузей науки.

У множині раціональних чисел (на відміну від цілих) завжди здійснене ділення, крім ділення на 0. Цікаво, що історично проблему щодо ділення було вирішено значно раніше, ніж проблему щодо віднімання, так що спочатку множину натуральних чисел (разом з нулем) було розширено до множини невід'ємних раціональних чисел, і лише потім з'явилися від'ємні числа. Справді, дроби набагато "реальніші", ніж від'ємні числа, перші простіше безпосередньо відчути на життєвих прикладах. Однак, з точки зору математики виглядає дещо природнішим спочатку сконструювати цілі від'ємні числа, а вже потім - дробові. Для шкільної програми в цьому питанні характерним є "історичний" підхід: учнів ознайомлюють з дробами раніше, ніж з від'ємними числами.

Множина всіх раціональних чисел позначається $\mathbb{Q}$ .

Дійсні числа

Назва чисел відображає думку про те, що вони дають змогу описувати дійсність (реальність). Після появи раціональних чисел стало зрозумілим, що вони не дають змогу вирішити всі задачі, які постали перед людством. Серед них такі задачі, як вимірювання відстаней (наприклад, діагоналі одиничного квадрата), пошук коренів квадратних рівнянь та ін. Було введено поняття ірраціонального (нераціонального) числа - числа, яке не може бути виражене за допомогою відношення цілих чисел. Сукупність раціональних та ірраціональних чисел утворює множину дійсних чисел.

Найпоширеніше позначення дійсних чисел - у вигляді десяткових (можливо нескінченних) дробів. Ірраціональні числа в цьому випадку - неперіодичні, нескінченні десяткові дроби. Зазначимо, що нескінченний десятковий дріб можна трактувати як послідовність певних скінченних десяткових дробів (тобто раціональних чисел); границя такої послідовності дорівнює числу, яке зображує цей десятковий дріб.

У множині дійсних чисел (на відміну від раціональних) завжди здійсненна дія добування кореня натурального степеня з невід'ємного числа.

Множина дійсних чисел позначається $\mathbb{R}$ , першою буквою слова "real" - дійсні.

Комплексні числа

Дослівний переклад назви цих чисел - "складені" ("складні") числа, від лат. "complex". Кожне комплексне число можна трактувати як пару дійсних чисел; якщо другий елемент цієї пари рівний 0, то таке комплексне число ототожнюють з дійсним (унаслідок чого маємо справді розширення множини дійсних чисел). Ті комплексні числа, які не ототожнені з жодним дійсним числом, називаються уявними числами (хоча існують і інші точки зору на значення словосполучення "уявне число").

Комплексні числа застосовуються в електродинаміці, квантовій механіці та інших галузях фізики.

У множині комплексних чисел завжди здійсненна дія добування кореня довільного натурального степеня з довільного комплексного числа (в той час як, залишаючись у межах дійсних чисел, корінь парного степеня можна добути лише з невід'ємного числа). Як наслідок, стає можливим розв'язати довільне квадратне рівняння (тобто навіть з від'ємнимдискримінантом).

Комплексні числа плідно використовуються також для розв'язування кубічних рівнянь (за формулами Кардано). Цікаво, що при цьому часто навіть для отримання дійсних розв'язків кубічного рівняння доводиться мати справу з уявними числами на деяких етапах розв'язування.

Множина комплексних чисел позначається $\mathbb{C}$ , першою буквою слова "complex" - комплексний.

Інші типи чисел

Комплексні числа можуть бути розширені до кватерніонів, від лат. "quattro" ("чотири"); кватерніон можна трактувати як упорядковану множину чотирьох дійсних чисел. Множина кватерніонів позначається $\mathbb{H}$ . Для кватерніонів втрачаєтьсякомутативність множення.

В свою чергу, октоніони $\mathbb{O}$ є розширенням кватерніонів і втрачають властивість асоціативності.

Кватерніони та октоніони є прикладами гіперкомплексних чисел.

Таким чином, вищерозглянуті множини чисел можна записати у вигляді такого ланцюжка: $\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}\subset \mathbb{C}\subset \mathbb{H}\subset \mathbb{O}$ .

У математиці існує поняття "потужність множини", яке є узагальненням поняття "кількість елементів множини" на випадок, коли множина може бути нескінченною. Для описання цих потужностей вводять кардинали або, що те саме, кардинальні числа.

Арабська система числення

Матеріал з Вікіпедії — вільної енциклопедії.

Порівняння зображень європейського, арабо-індійського, східного арабо-індійського, деванагарі та тамільського написання цифр

Ара́бською систе́мою чи́слення називають десять символів: 0 1 2 3 4 5 6 7 8 9, за допомогою яких записується в десятковій системі числення будь-якечисло. Арабські цифри виникли в Індії і в 10—13 ст. були занесені в Європу арабами (звідси й назва).

Згідно з популярною традицією, що досі поширена в Єгипті і Північній Африці, «Арабські» цифри є винаходом скляра-геометрика. Він вважав, що дев'ятьом цифрам потрібно надати форму, яка відповідала б їхньому значенню і пропонував для цього фігури з відповідною кількістю кутів. Якщо зробити певні переміщення цих фігур, то вони разом складуть арабський вислів:Моя ціль — обчислення (араб. وهدَفي حسابْ)

[ред.]Походження

Дані символи і спосіб їх використання європейці запозичили у Середні віки у мусульманських математиків (рівень математики арабських країн на той час був вищий, ніж у європейців), звідси і походить назва арабські цифри. Насправді араби запозичили їх у індійців. Індійські математики користувались дещо іншими символами, і ті символи, якими користуємось ми, є результатом тривалої зміни їхнього первісного вигляду. Цифри, які називають арабськими, відрізняються від цифр, якими користуються в арабських та індійських країнах.

Особливості

Особливістю арабської системи цифр є позиційна десяткова система числення — вага кожної цифри визначається положенням у числі. Наприклад, у числі 38235 є дві цифри 3, однак вони відрізняються за значенням — цифра 38235 означає три десятки, а цифра 38235 — тридцять тисяч.

До запозичення арабських цифр європейці користувались римськими цифрами, де десятки, сотні і тисячі позначались спеціальними знаками, а також не було символу нуля.

Нуль — друга особливість арабської системи цифр. Є дані, які вказують, що шумеривикористовували у своїй шістдесятковій системі числення знак, що мав зміст нуля. Однак знайдено лише кілька записів, що містять цей знак. У арабській системі нуль є важливим елементом, оскільки при позиційній системі числення недопустимим є пропуск розряду.

Міфічне число - це число, яке вживається та приймається начебто як результат наукового дослідження і/або спостереження, але, насправді, походження якого достеменно невідоме і достеменність якого не обґрунтована. Термін було введено 1971 року Максом Сінгером, одним з засновників Інститута Гудзона.

Відомі приклади: твердження, що людина використовує лише 10% від потужності власного мозку, рекомендація жувати їжу 29 разів перед ковтком, правило п'яти секунд.

Виникнення таких чисел споріднене з виникненням міських легенд і може, між іншим, ґрунтуватися на:

невірній інтерпретації прикладів
екстраполяції прикладів з інших галузей знань
результатах комічних дослідів
різних дезінформаціях
припущеннях відомих людей
вдалих жартах

Нумероло́гія — сукупність вірувань та практик, які приписують числам певні властивості в залежності від культурного чи історичного контексту. Нумерологія є так званою псевдонаукою.

У нумерології всі числа можуть бути зведені до одиничних розрядів, які відповідають певним окультним характеристикам, що нібито впливають на життя людини. Тобто в певній нумерологічній системі за кожним однозначним числом закріплені певні властивості, поняття та образи. Нумерологією користуються при аналізі характеру людини, намагаючись таким чином визначити характер, природні обдарування, сильні та слабкі сторони, передбачити майбутнє, вибрати краще місце для життя, роботи, вирахувати найбільш пасуючий час для прийняття рішень і для дій. Деякі люди послуговуються нумерологією, щоб вибрати собі партнерів — у бізнесі, шлюбі, а також в товаристві.

Діякі прихильники теорій змови надають числам особливого значення (пор. значення числа 23 в романах Іллюмінатус!) У СШАнерідко й досі пропускають число 13 при нумерації поверхів, тринадцятий поверх позначається як 12а або зразу 14. Часом опускання «нещасливого» числа 13 можна зауважити і в літаках чи на пароплавах, та само й у лікарнях часто відсутня палата № 13. У столиці Нової Зеландії Веллінгтоні на тринадцятих поверхах будинків часто розташовані адміністративні служби, оскільки оренда приміщень для фірм чи приватних осіб досить проблематична лише через «нещасливий» номер.

Часом прихильники нумерології висувають твердження, що певні символічні числа відтворюють природні закономірності світобудови чи окремих реальних структур природного світу, ба навіть уможливлюють передбачення і пояснення певних подій. Такі твердження можна перевірити лише науковим шляхом, насамперед за допомогою статистичних методів. У більшості випадків дані нумерології є надто неточними і не підтверджуються дослідним шляхом. Нумерологія як псевдонаука має наукоподібну форму, але не відповідає критеріям наукової теорії. Так, наприклад, нумерологічні прогнози можуть стосуватися надто великого числа майбутніх подій, отже нумерологічні гіпотези в цьому випадку є надто розпливчастими й неточними, вони мають занадто мало обмежень, які можна було б перевірити емпіричним (дослідним) шляхом.^[1]

Нідерландський асторфізик Корнеліс де Ягер виступив з фундаментальною критикою гіпотез, в яких ненауковим чином поєднуються асторфізичні та геофізичні дані і які пропонують висновки про приховану символіку чисел у таких давніх спорудах, як, наприклад, Піраміда Хеопса. Такими є зокрема твердження так званої «пірамідології». За де Ягером, достатньо простенької комп'ютерної програми, аби знайти комбінації чисел, що створюватимуть враження своєї невипадковості. Аби проілюструвати свою тезу де Ягер запропонував пародійний приклад вигаданої ним «велосипедософії», яку він обґрунтовує за допомогою позірних «прихованих відповідностей» між параметрами власного велосипеда (діаметр деяких деталей) та фізичними константами, зокрема гравітаційною сталою.

Систе́ма чи́слення (англ. number (numeration) system, notation) - сукупність способів і засобів запису чисел для проведення підрахунків.

Розрізняють такі типи систем числення:

позиційні
змішані

непозиційні

Двійкова система	Шістнадцяткова система	Десяткова система
00000	00	00
00001	01	01
00010	02	02
00011	03	03
00100	04	04
00101	05	05
00110	06	06
00111	07	07
01000	08	08
01001	09	09
01010	0A	10
01011	0B	11
01100	0C	12
01101	0D	13
01110	0E	14
01111	0F	15
10000	10	16
10001	11	17
10010	12	18
10011	13	19
10100	14	20
10101	15	21
10110	16	22
10111	17	23
11000	18	24
11001	19	25
11010	1A	26
11011	1B	27
11100	1C	28
11101	1D	29
11110	1E	30
11111	1F	31

У позиційних системах числення одна і та ж цифра (числовий знак) у записі числа набуває різних значень залежно від своєї позиції. Таким чином, позиція цифри має вагу у числі. Здебільшого вага кожної позиції кратна деякому натуральному числу 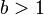$b$ , $b>1$ , яке називається основою системи числення.

Наприклад, якщо b - натуральне число ( 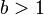$b > 1$ ), то для представлення числа x у системі числення з основою b його подають у вигляді лінійної комбінації степенівчисла b:

$x = \sum_{k=0}^n a_k b^k$ , де $a_k$ — цілі, $0 \leq a_k < b$

Іншими словами, основа - це кількість символів, що використовуються при записуванні чисел.

Приклад

Наприклад, число «двісті чотири» представляється у десятковій системі числення у вигляді:

$204 = 2 \cdot 10^{2} + 0 \cdot 10^{1} + 4 \cdot 10^{0}$

Використовуючи позиційний принцип, можна зобразити будь-яке дійсне число за допомогою усього лиш десяти цифр у їх різних комбінаціях.

Змішана система

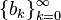Змішана система числення є узагальненням системи числення з основою $b$ і її часто відносять до позиційних систем числення. Основою змішаної системи є послідовність чисел, що зростає, $\{b_k\}_{k=0}^{\infty}$ і кожне число $x$ представляється яклінійна комбінація:

$x = \sum_{k=0}^n a_{k}b_k$ , де на коефіцієнти $a_{k}$ (цифри) накладаються деякі обмеження.

Якщо $b_k=b^k$ для деякого $b$ , то змішана система збігається з $b$ -основною системою числення.

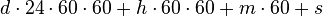Найвідомішим прикладом змішаної системи числення є представлення часу у вигляді кількості діб, годин, хвилин і секунд. При цьому величина d днів h годин m хвилин s секунд відповідає значенню $d\cdot 24\cdot 60\cdot 60 + h\cdot 60\cdot 60 + m\cdot 60 + s$ секунд.

Система числення Фібоначчі

Представлення засновується на числах Фібоначчі:

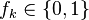$x = \sum_{k=0}^n f_k F_k$ , де $F_k$ — числа Фібоначчі, $f_k\in\{0,1\}$ , при цьому у записі $f_nf_{n-1}\dots f_0$ не зустрічаються дві одиниці підряд.

Представлення використовує факторіал натуральних чисел:
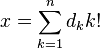$x = \sum_{k=1}^n d_k k!$ , де $0\leq d_k \leq k$ .

Біноміальна система числення

Представлення використовує біноміальні коефіцієнти: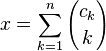

$x = \sum_{k=1}^n {c_k\choose k}$ , де $0\leq c_1 < c_2 < \dots < c_n$
Система числення майя

Майя використовували двадцяткову систему числення за одним винятком: у другому розряді було не 20, а 18 ступенів, тобто після числа (17)(19) відразу йшло число (1)(0)(0). Це було зроблено для полегшення розрахунків календарного циклу, оскільки (1)(0)(0) дорівнювало 360, що приблизно дорівнює кількості днів у сонячному році.
Позиційна система числення

У непозиційних системах числення величина, яку позначає цифра, не залежить від позиції її у числі. При цьому система може накладати обмеження на позиції цифр, наприклад, щоб вони були розташовані по спаданню, чи згруповані за значенням. Проте це не є принциповою умовою для розуміння записаних такими системами чисел.

Типовим прикладом непозиційної системи числення є римська система числення, в якій у якості цифр використовуються латинські букви:

Римська цифра	Десяткове значення
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

Наприклад, VII = 5 + 1 + 1 = 7. Тут символи V і I означають 5 і 1, відповідно, незалежно від місця їх у числі.

Застосування

У нумізматиці особливо велику вагу мають десяткова система, дванадцяткова (дуодецимальна), четвертна та шісткова системи. У інформаційних технологіях застосовуються двійкова, десяткова, вісімкова, та шістнадцяткова системи.

Улюблені числа жителів Атлантиди

Атлантида! Скільки легенд та оповідань пов’язано з цією казковою державою, “золотого століття цивілізації”. Багато цікавого про неї розповідав в своїх “Діалогах” стародавньо грецький філософ і математик Платон.

Платон дуже часто згадував число шість. Напевне у жителів Атлантиди це число було в пошані.

В стародавній Греції , в школі Піфагора, з трепетом відносилися до числа 28. Нещодавно В Римі під час будування метро під землею було знайдено цікавий ансамбль кімнат: круглий зал і навколо нього 28 кімнат, що виходять у цей зал. Виявилось, що це приміщення неопіфагорійської академії, яка існувала в Римі в перші століття нашої ери. Напевне в цій академії було 28 членів. І до сих пір число членів деяких академій та наукових товариств дорівнює 28.

У римлян на святах найпочеснішим місцем було-шосте.

Чим же притягувало жителів Атлантиди і жителів “вічного” міста Риму число 6, чому піфагорійці віддавали особливу перевагу числу 28?

Ці числа об’эднуэ одна особлива власти

вість: сума всіх їх дільників дорівнює самому числу: 6=1+2+3; 28= 1+2+4+7+14.Крім 6 і 28 стародавні греки знали ще два числа , які мають такіж властивості—496 та 8128.Ідеальні числа зустрічаються дуже рідко. Лише в XY ст. було знайдено ще два ідеальних числа німецьким математиком Іоганном Мюллером.Сьоме число знайшов в 1883 році сільський священник Іван Міхєєвич Первушин

В наш час відомо лише 20 ідеальних чисел. Двадцяте ідеальне число містить 2663 цифри.

Математика

Сторінки

Число

Число

Типи чисел

Історія натуральних чисел

Алгебраїчні властивості

Теоретико-множинні властивості

Ознаки подільності чисел в десятковій системі

Дійсні числа

Комплексні числа

Інші типи чисел

Арабська система числення

[ред.]Походження

Особливості

Змішана система

Система числення Фібоначчі

Біноміальна система числення

Система числення майя

Застосування

Немає коментарів:

Дописати коментар