Математика - цариця всіх наук

Матема́тика (грец. μάθημα — наука, знання, вивчення) — наука, яка первісно виникла як один з напрямків пошуку істини (у грецькій філософії) у сфері просторових відношень (землеміряння — геометрії) і обчислень (арифметики), для практичних потреб людини рахувати, обчислювати, вимірювати, досліджувати форми та рух фізичних тіл. Пізніше розвинулась у досить складну і багатогранну науку про абстрактні кількісні та якісні співвідношення, форми і структури. Загальноприйнятого визначення математики немає. Початково вона використовувалася для підрахунку,вимірювання, а також для вивчення форм і руху фізичних об'єктів шляхомдедуктивних розмірковувань та абстракцій. Математики формулюють нові висновки і намагаються встановити їх справедливість, виходячи зі вдало вибраних аксіом і визначень.

Евклід, математик що жив у Давній Греції в3 ст. до н. е. роботи Рафаеля

Математика виникла з давніх-давен з практичних потреб людини, її зміст і характер з часом змінювались. Від початкового предметного уявлення про ціле додатне число, від уявлення про відрізок прямої, як найкоротшу відстань між двома точками. Математика пройшла довгий шлях розвитку, перш ніж стала абстрактною наукою з точно сформованими вихідними поняттями і специфічними методами дослідження. Нові вимоги практики, розширюють обсяг понять математики, наповнюють новим змістом старі поняття.

Поняття математики абстраговані від якісних особливостей специфічних для кожного даного кола явищ і предметів. Ця обставина дуже важлива у застосуванні математики. Так, число 2 не має якогось певного предметного змісту. Воно може відноситися і до двох книг, і до двох верстатів, і до двох ідей. Воно добре застосовується і до цих і до багатьох інших об'єктів. Так само геометричні властивості кулі не змінюються від того, зроблено її зі сталі, міді чи скла. Звичайно, абстрагування від властивостей предмету збіднює наші знання про цей предмет і його характерні матеріальні особливості. В той же час саме це абстрагування надає математичним поняттям узагальненості, даючи можливість застосовувати математику до найрізноманітніших за природою явищ. Це означає, що одні й ті ж закономірності математики, один і той же математичний апарат можуть бути достатньо успішно застосовані до біологічних, технічних, економічних та інших процесів.

Розвиток математики опирається на писемність і вміння записувати числа. Напевно, стародавні люди спочатку висловлювали кількість шляхом малювання рисок на землі або видряпували їх на деревині. Стародавні інки, не маючи іншої системи писемності, представляли і зберігали числові дані, використовуючи складну систему мотузяних вузлів, так звані кіпу. Існувало безліч різних систем числення. Перші відомі записи чисел були знайдені в папірусі Рінда, створеному єгиптянами Середнього царства.Індська цивілізація розробила сучасну десяткову систему числення, що включає концепцію нуля.

Абстрагування в математиці не є її винятковою особливістю, оскільки всілякі загальні поняття містять в собі деякий елемент абстрагування від властивостей конкретних речей. Але в математиці цей процес йде далі, ніж у природничих науках. У ній широко використовують процес абстрагування різних ступенів. Наприклад, поняття групивиникло внаслідок абстрагування від деяких властивостей чисел та інших уже абстрактних понять. У математиці специфічним є також метод одержання результатів. Якщо природознавець, доводячи будь-яке твердження, завжди використовує дослід, то математик доводить свої результати лише на основі логічних міркувань. Жодний результат у математиці не можна вважати доведеним, поки йому не дано логічногообґрунтування, хоч спеціальні досліди і підтвердили його. В той же час істинність математичних теорій перевіряється на практиці, але ця перевірка має особливий характер. Висуваються математичні теорії реальних явищ, а висновки з цих теорій перевіряються на досліді. Однак зв'язки математики з практикою є ширшими, бо поняття математики: теореми, задачі, математичні теорії пов'язані із запитами практики. З часом ці зв'язки стають глибшими і різноманітнішими. Математику можна застосувати до вивчення будь-якого типу руху. Проте в дійсності її роль в різних галузях наукової і практичної діяльності неоднакова. Особливо великою є роль математики у вивченні тих явищ, для яких навіть значне абстрагування від їхніх специфічних якісних характеристик не змінює істотно притаманних цим явищам кількісних і просторовихзакономірностей. Наприклад, у небесній механіці тіла вважають матеріальними точками (тобто абстрагуються від реальності); обчислені таким способом рухи небесних тіл збігаються з дійсними рухами цих тіл. Користуючись математичним апаратом, можна не тільки дуже точно передобчислювати небесні явища (затемнення, положення планет тощо), але й за відхиленням істинних рухів від обчислених зробити висновок про наявність невидимих неозброєним оком небесних тіл. Саме так було відкрито планети Нептун (1846) і Плутон (1930). У зв'язку з бурхливим розвитком космічних польотів небесна механіка набула все більшого значення. Механіка і фізика стали, по суті, математичними науками. Менше, але все ж значне місце посідає математика в економіці, біології, медицині, лінгвістиці. Для цих наук особливого значення набула математична статистика. Якісна своєрідність явищ, що вивчаються, наприклад, у біології, настільки значна, що роль математичного аналізу придослідженні їх поки що є підпорядкованою. Процес математизації наук, що почався з 18 ст., тепер набув винятково інтенсивного розвитку.

Історію математики вчені зазвичай поділяють на чотири періоди:

• період зародження математики як самостійної дисципліни — тривав приблизно до 6—5 століття до н. е. В цей період формувались поняття цілого числа і раціонального дробу, поняття відстані, площі, об'єму, створювались правила дій з числами та найпростіші правила для обчислення площ фігур і об'ємів тіл. Математика не мала ще форми дедуктивної науки, вона являла собою збірник правил для виконання певного роду дій. У всіх математичних текстах (єгипетських,вавилонських), що дійшли до нас, математичні знання викладалися саме в такій формі.
• період елементарної математики — тривав від 6—5 ст. до н. е. до середини 17 століття. В цей період на основі невеликої кількості вихідних тверджень — аксіом будувалася геометрія як дедуктивна наука. Математика перестала бути безіменною наукою. З історії математики відомі імена багатьох вчених давньої Греції (Фалес, Піфагор, Гіппократ Хіоський, Демокріт,Евдокс, Евклід, Архімед та ін.), Китаю (Чжан Цан, Ген Шоу-чан, Цзу Чун-чжі та ін.), Середньої Азії (Джемшід ібн-Масуд аль-Каші, Мухаммед бен-Муса аль Хорезмі та ін.), Індії і пізніше Західної Європи (Лодовіко Феррарі, Нікколо Тарталья,Джироламо Кардано, Сімон Стевін та ін.), що зробили значний вклад у математику.
• Третій період (середина 17 ст. — початок 20 ст.) — період дослідження змінних величин. Природознавство і технікадістали новий метод вивчення руху і зміни — диференціальне числення та інтегральне числення. Створився ряд нових математичних наук — теорія диференціальних рівнянь, теорія функцій, диференціальна геометрія, варіаційне числення та ін., що значно розширили предмет і можливості математики. Велику роль у розвитку математики цього періоду відіграли й українські математики. Микола Лобачевський відкрив неевклідову геометрію, Михайло Остроградський зробив визначні відкриття в механіці, математичному аналізі, математичній фізиці, Пафнутій Чебишов поклав початок новому напряму в теорії функцій, зробив значні відкриття в теорії чисел, теорії імовірностей, механіці, наближеному аналізі. До цього ж періоду відноситься діяльність таких видатних вчених, як Олександр Ляпунов, Андрій Марков (старший), Георгій Вороний та багатьох інших.
• Четвертий період — період сучасної математики — характеризується свідомим і систематичним вивченням можливих типів кількісних співвідношень і просторових форм. У геометрії вивчається вже не лише тривимірний простір, а й ін. подібні до нього просторові форми. Характерними напрямами розвитку математики цього періоду є теорія множин, функціональний аналіз, математична логіка, сучасна алгебра, теорія імовірностей, топологія тощо.

З 17 століття розвиток математики істотною мірою взаємокоординується з розвитком фізики, механіки, низки технічних дисциплін, зокрема гірництва. Математика широко застосовується, наприклад, для складання та опрацювання математичних моделей технологічних процесів.

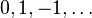Натуральні числа	Цілі числа	Раціональні числа
Дійсні числа	Комплексні числа	Кватерніони

Перетворення

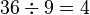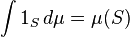Арифметика	Диференціальне та інтегральне числення	Векторний аналіз	Математичний аналіз
Диференціальні рівняння	Динамічні системи	Теорія хаосу

Структури

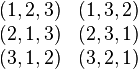Комбінаторика	Теорія чисел	Теорія груп	Теорія графів	Теорія порядку

Просторові відношення

Дослідження простору спричинило до виникнення геометрії, зокрема Евклідової геометрії. Тригонометрія — це розділ математики, що має справу з відношеннями між сторонами та кутами в трикутнику та з тригонометричними функціями; тут простір виражений в числах, до цього розділу входить знаменита Теорема Піфагора. Сучасні дослідження простору узагальнюють ці ідеї та включають багатовимірну геометрію, неевклідові геометрії (які грають центральну роль в загальній теорії відносності) та топологію. Кількісні та просторові характеристики разом досліджуються в аналітичній геометрії, диференціальній геометрії та алгебричній геометрії. Конвексна геометрія та дискретна геометрія були розроблені, щоб розв’язати задачі в теорії чисел та функціональному аналізі, але тепер знайшли своє застосування в оптимізації та інформатиці.

Геометрія	Тригонометрія	Диференціальна геометрія	Топологія	Фрактальна геометрія

Геометрія — Тригонометрія — Алгебрична геометрія — Топологія — Диференціальна геометрія — Диференціальна топологія — Алгебрична топологія — Лінійна алгебра — Фрактальна геометрія

[ред.]Дискретна математика

Дискретна математика містить засоби, які застосовуються до об'єктів, що можуть приймати лише специфічні, окремі значення (не неперервні).

Теорія множин	Математична логіка	Теорія обчисленності	Криптографія	Теорія графів

Крилаті вислови
З усіх істинних наук, як твердять Арістотель і Авероес, наші математичні науки найістинніші і мають перший ступінь вірогідності, решта природничих наук іде за ними.
ЛI. Пачолі

Ніякої достовірності нема в науках там, де не можна застосувати ні однієї з математичних наук, і в тому, що не має зв'язку з математикою.
Леонардо да Вінчі

Сама лише математика має неспростовні докази, що виходять із необхідних причин. Через це тільки там людина може, спираючись на власні закони цієї науки, підійти до істини.
Р. Бекон

У самій лише математиці є наука і доведення у найточнішому і власному розумінні.
Гросетес

Все має бути доведеним, і при доведенні не можна послуговуватись нічим, крім аксіом і раніше доведених теорем.
Б. Паскаль

У математичних питаннях не можна нехтувати й найменшими похибками.
І. Ньютон

Люди, не знайомі з алгеброю, не можуть уявити собі тих дивних речей, яких можна досягти за допомогою названої науки.
Г. Лейбніц

Саме математика насамперед захищає нас від обману чуттів і вчить, що одна справа —як влаштовані предмети, які сприймаються чуттями, а інша — якими вони здаються; ця наука дає найнадійніші правила; хто керується ними, тому не страшний обман чуттів.
Л. Ейлер

Математику вже навіть задля того треба вивчати, що вона розум до ладу приводить.
М. В. Ломоносов

Перша умова, якої треба дотримуватися у математиці,— це бути точним, друга — бути ясним і, наскільки можливо, простим.
Л. Карно

Математика — цариця всіх наук. її улюблениця — істина, її вбрання — простота і ясність. Палац цієї володарки оточено тернистими заростями, і, щоб досягти його, кожному доводиться пробиратися крізь хащі. Випадковий мандрівник не виявить у палаці нічого привабливого. Краса його відкривається лише розуму, що любить істину і загартований в боротьбі з труднощами, і такому, який свідчить про незвичайну схильність людини до заплутаних, але невичерпних і піднесених розумових насолод.
Ян. Снядецький

Передусім... слід зрозуміти поняття, що лежать в основі слів, для того щоб, зводячи до них наші думки, питання, вагання, ми могли обговорювати їх і щоб у нас при нескінченних поясненнях нічого не залишалося нерозв'язаним, або щоб ми не мали порожніх слів.
Епікур

Розв'язування софізмів, які призводять до абсурдів, для не новачка в математиці повинні бути чудовим засобом перевірки правильності наближення до математичної істини, засобом тренування розуму і удержування міркування й доказів у твердо встановлених межах.
Ж. Віола

Тисячі шляхів ведуть до помилки, до істини — тільки один.
Ж.Ж. Руссо

Математика — дивовижна вчителька в мистецтві спрямовувати думки, наводити порядок там, де вони не впорядковані, викорчовувати безглуздя, фільтрувати брудне і наводити ясність.
Ж. Фабр

Дуже важливо не приймати ніяких припущень без доведення, а ще важливіше не користуватися словами, якщо їм не надано певного смислу.
В. Кліффорд

Дуже помилковою є думка... що строгість в доведенні— це ворог простоти. Численні приклади переконують нас у протилежному: строгі методи є одночасно і найпростішими, і найдоступнішими. Прагнення до строгості саме й приводить до знаходження найпростіших доведень.
Д. Гільберт

З тих пір як почали доводити очевидні твердження, багато з них виявилися хибними.
Б. Рассел

Доведення, яке не є строгим,— це ніщо.
А. Пуанкаре

У математичній науці все, що не обґрунтовано до кінця, розцінюється як абсолютно необґрунтоване.
С. Я. Хінчин

Для математики характерним є доведення до крайньої межі домінування логічної сили міркування; математик, який, бодай тимчасово, опустить цю схему, взагалі втрачає здатність науково мислити.
О. Я- Хінчин

У математиці немає і не може бути «напівдоведених» і «майже доведених» тверджень: або повноцінність аргументації — така, що ніякі суперечки про правиль­ність доводжуваного твердження вже неможливі, або аргументація взагалі відсутня.
О. Я- Хінчин

У моральному плані математика навчає нас суворо ставитися до того, що стверджується як істина, що висувається як аргумент чи висловлюється як доведен­ня. Математика вимагає ясності понять та тверджень і не терпить ні туману, ні бездоказових заяв.
О. Д. Александров

Математичне доведення наводиться так скрупульозно, що воно стає незаперечним і переконливим для кожного, хто тільки його зрозуміє... Однак строгість математики не абсолютна: вона розвивається, принципи математики не застигли раз назавжди, а рухаються і теж можуть бути і є об'єктом наукових суперечок.
О. Д. Александров

Серед усіх наук математика користується особливою повагою; підставою для цього є та єдина обставина, що її положення абсолютно правильні й незаперечні, в той час як положення інших наук до деякої міри спірні, і завжди є небезпека їх спростування новими відкриттями.
А. Ейнштейн

Ніде, як у математиці, ясність і точність умовиводу не дають змоги замінити відповідь розмовами навколо питання.
О. Д. Александров

Математика навчає точності думки, підкоренню логіці доведень, поняттю строго обґрунтованої істини, а все ж формує особистість, мабуть, більше, ніж музика.
О. Д. Александров

Неспростовність — ім'я твоє, математика. Нехай представник природничих наук задовольняється очевидністю— математикові потрібні докази.
У. В. Куайн

Ми, математики, маємо напрочуд простий критерій істини. Доведення або є, або його немає.
К. Урбанік

У математиці немає авторитетів. Єдиний аргумент істинності — доведення.
К- Урбанік

Поняття істинності майже неминуче потребує абстракції нескінченності вже тому, що правильне математичне висловлювання має бути правильним завжди і всюди.
Ю. І. Манін

Для строгого логіка неповне доведення — взагалі не доведення. І, звичайно, потрібно чітко розмежовувати неповні й повні доведення. Плутати їх одне з одним погано, а ще гірше приймати одне за друге.
Д. Пойа

Потрібно всіма засобами навчати мистецтву доведення, не забуваючи при цьому про мистецтво здогадуватися.
Д. Пойа

Математика дає найбільш чисте й безпосереднє переживання істини; на цьому ґрунтується її цінність для загальної освіти людей.
М. Лауе

Строгість у математиці означає насамперед добросовісніссність.
Ліпман Бере